Steady Ticking
Почти все видео-игры (и, следовательно, игровые движку) имеют в общем случае технику итерирования игрового процесса. Игра по сути является циклом. Это цикл так и называется - игровой цикл. В каждой итерации игрового цикла игра должна приготовить и актуализировать своё состояние, в частности, проработать рендеринг, оценить производительность и нарисовать графику. В рамках Unreal Engine эти итерации называются тиками (ticks). Это что-то наподобие сердца игры.
Как и сердцебиение человека, временные интервалы тиков различаются; то есть изменяется время, необходимое для того, чтобы обработать и отрисовать новый кадр. Вы можете неожиданно получить кадр, вычислительная или графическая нагрузка на котором будет достаточно высокая, и время тика увеличится.
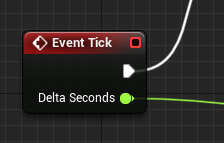
Чтобы игровая логика актуализировала состояние игры, этот меняющийся временной интервал (delta time) подаётся ей на вход как вещественное значение, чтобы построить новый «шаг» на основе предыдущего. В Unreal Engine это делается при помощи ноды-события Tick, а конкретно, при помощи её аргумента Delta Seconds:
Техника рабочая, например, когда вы играете в игру с заранее вычисленной анимацией, где результат всегда определён во времени. К несчастью, так бывает не всегда, так как игры в большинстве своём интерактивны и нагрузка меняется от кадра к кадру.
Если применить переменное время кадра к такому процессу, как просчитывание коллизий, то их устойчивость будет значительно падать, если время тика увеличится. Рассмотрим следующий пример.
Пусть у нас есть шар с симуляцией физики. Шар сдвигается со своей позиции в зависимости от своей скорости (которая определяется на основе гравитации и других действующих сил). Когда время тика стабильно и достаточно мало, всё работает, как ожидалось. Но как только один из кадров «даёт сбой», система сразу же становится крайне нестабильной и мяч с лёгкостью может проскочить сквозь пол, что приводит к совершенно некорректному поведению.
Наша цель - стабилизировать время кадра и нормализовать вычисления.
В физике Unreal Engine есть способ стабилизировать время кадра. Это достигается ограничением максимального времени тика:

Если текущий кадр занимает большее время, чем заданное значение, физика движка получит это значение как свой delta time, для вычисления текущего шага. Это, в свою очередь, вызовет в замедление игрового времени. Что-то наподобие slow-mo эффекта, а симуляция не потеряет своей стабильности, то есть, стабильность будет не ниже, чем предоставленное допустимое значение.
Другой способ достичь стабильности физики - использовать такую технику Unreal Engine, как sub-stepping. Для большей информации по этой теме можете посмотреть официальную документацию по ссылке.
Apparatus предоставляет схожую sub-stepping-гу концепцию, которую мы называем «Steady Ticking». Каждый Mechanism реализовывает специальное событие Steady Tick:
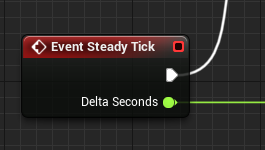
Устойчивые тики имеют фиксированный временной интервал и выполняются параллельно основным тикам (event-tick), у которых этот интервал может меняться. Слово «параллельно» совершенно не означает мульти-поточность, напротив, подчёркивает логику вызовов.
На картинке выше вы могли заметить, что может произойти несколько устойчивых тиков за один переменный тик. Также, как и несколько переменных тиков могло произойти за один устойчивый. Такие различия могут привести к нежелательным резким перемещениям объектов (или выполнения другой логики). Чтобы решить этот вопрос нужна интерполяция.
В течение переменного «родного» тика мы интерполируемся между предыдущим устойчивым тиком и следующим. Сам пользователь может выполнять необходимую интерполяцию, но Apparatus уже предоставляет требуемый функциональный базис, чтобы это сделать.
Для начала рассмотрим ноду Steady Frame Ratio (соотношение устойчивых кадров):
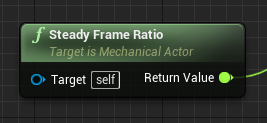
Эта нода возвращает отношение текущего переменного тика к активному устойчивому. Для лучшего понимания, просто посмотрите эту схему:
Это отношение, являясь числом из отрезка [0.0, 1.0], может быть использовано для интерполяции анимации на основе её предыдущей и следующей состояний. Чтобы этого достичь, ваши механики, выполняемые устойчивыми тиками, должны подготовить оба эти состояния в течении своего времени выполнения. Обычный же (переменный) тик может использовать ноду Lerp, чтобы обеспечить непосредственно гладкость и неразрывность.
Иногда бывает утомительно (или довольно трудно) управлять обеими предыдущим и следующим состояниями в некоторых вспомогательных переменных. Вы, возможно, захотите использовать текущее состояние объекта, вместо предыдущего, - например, можно использовать transform-вектор для вычисления следующего шага. Поэтому мы предлагаем вам метод, который удобно использовать и при таком подходе, - нода Steady Future Factor.
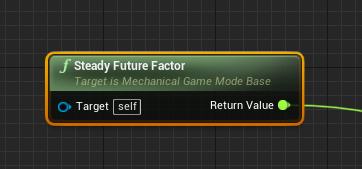
Эта нода несколько похожа на Steady Frame Ratio, по крайней мере тем, что возвращает единственное число с плавающей точкой из отрезка [0.0, 1.0]. Но отличается она, на самом деле, причиной, по которой выходные значения лежат именно в таком промежутке. Проиллюстрируем это на схеме:
Как вы можете видеть, последнее изменение (было оно в устойчивом или обычном тике) отслеживается и запоминается в качестве стартовой точки для отношения. Вторая часть такая же, как и для узла Steady Frame Factor, и фактически представляет собой временную метку следующего будущего устойчивого кадра/*не понял предложения, прогнал через Google-translate: The second part is the same as for the Steady Frame Factor node and actually represents a timestamp of the next future steady frame.*/. Используя ноду Steady Future Factor, вы можете использовать текущее актуальное состояние как базу для Lerp„а со следующим состоянием. Просто будьте внимательны к своим вычислениям и убедитесь в том, что в реально поддерживаете трек того, что вы хотите интерполировать.
Обе эти ноды могут быть использованы прямо в tick-событиях ваших механик. Однако, мы имплементировали специальное событие для механик, так называемое Presentation Tick-событие, которая естественным образом связывает вышеперечисленные pure-функции:
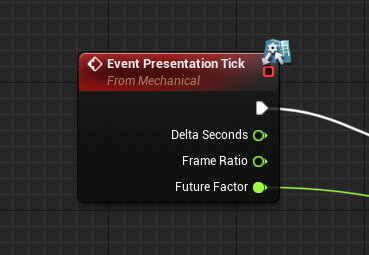
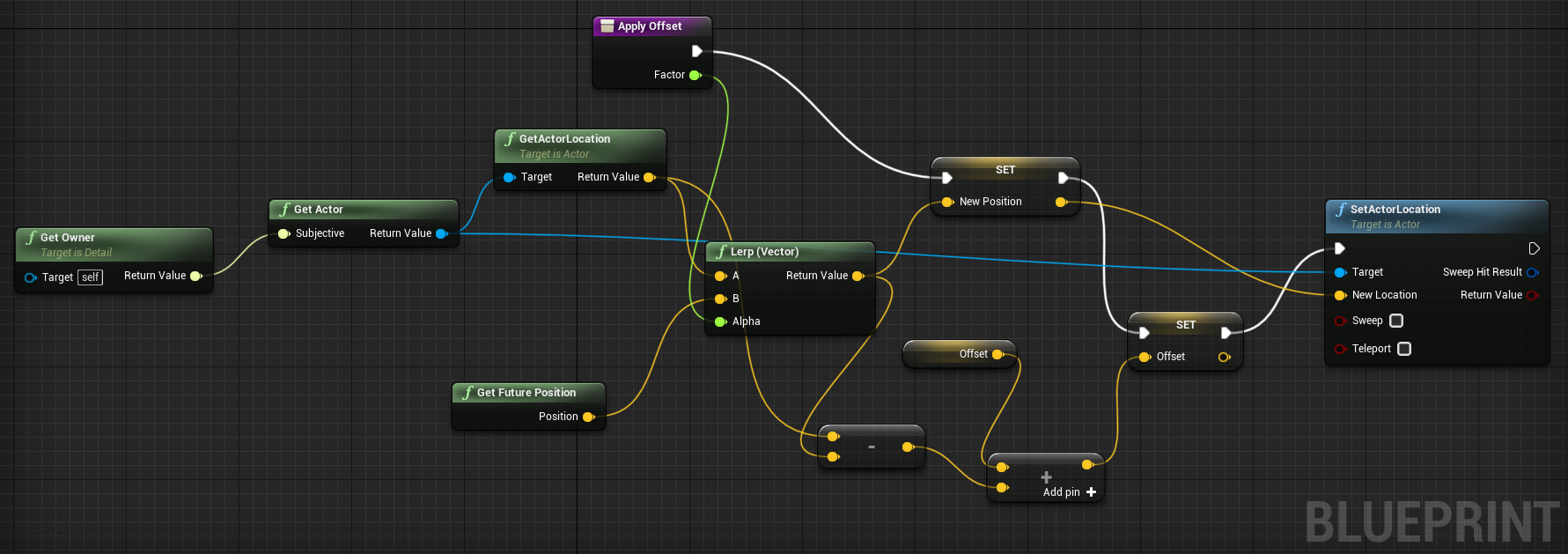
Это событие наступает после нормальных переменных тиков (а значит, и после тиков устойчивых) и подразумевает использование для вычисления визуального отклика механик. Интерполяция механик, очевидно, тоже может быть вычислена. Посмотрите на этот всеобъемлющий пример механики интерполяции 3d-положения объекта (выдержка из нашего примера-платформера):
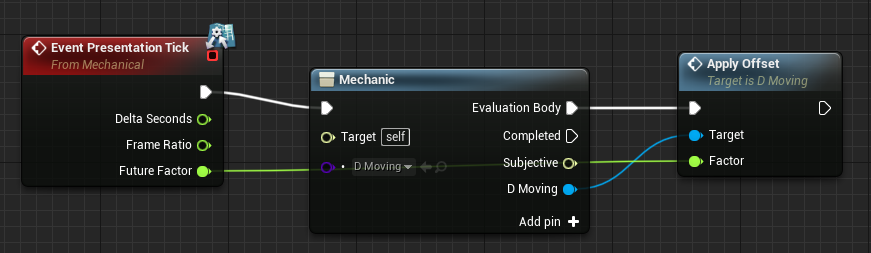
Самая важная Apply Offset функция выглядит так:
Завершая тему статьи, следовало бы сказать о том, что описанные техники вовсе не являются обязательными к применению. Вы можете выполнять свои механики так, как захотите, и настраивать движок так, чтобы он обрабатывал только определённые FPS. Мы же, тем не менее, предлагаем вам путь для достижения стабильной частоты кадров геймплея и также рекомендуем использовать его для поддержания стабильности.